Using angular distance to pinpoint an object in the night sky can mean zilch when you’re a newbie. The units mightn’t make sense. As a backyard astronomer the following handy guide is all about acquainting yourself and making it simple to understand…

…rather than use an app or astronomy book… you can use your hand to get an idea of space between objects or of their positioning. I show how in my infographic below.
About angular distance in astronomy
Angular distance measures a span you see in or of the sky. Example is the space between two celestial objects as observed from Earth or the positioning of a planet above the horizon.
You might come across angular distances when you are using a star map or an app such as Stellarium on your phone to find celestial objects. It’s the value given in degrees.
Why degrees are used distances in the sky
Degrees are used in measuring sky distances as well as the field of view of optics used in stargazing.
The following are fundamental reasons degrees make sense in taking in the sky we observe:
- The positioning system on land (latitude/longitude) involves degrees
- Celestial bodies can be pinpointed using a similar system of degrees (altitude/azimuth)
- The sky above is like a dome and the arc overhead (altitude), from one horizon to the opposite, is a semi-circle (180º). From horizon to zenith is 90º.
- Going horizontal from north to east to south to west and back to north is a circle (360º)

Angles are used for navigation: Sailors in the past would use the angle of Polaris above the horizon to work out their position for navigational purposes.
Coordinate system for the night sky
At a point in time a celestial body sits at an intersection of x number of degrees altitude and an x number of degrees azimuth, as observed by us.
Direct north is zero on the azimuth plane, where east is 90º, south 180º, and west 270º.
From the altitude/azimuth configuration (see also horizontal coordinate system) we can work out the exact position of celestial objects and find where planets sit in the night sky.
All of this helps in explaining the axis of alt/az telescope mounts.
measuring degrees in the sky with your hand
Hand measurements provide a no fuss angular separation calculator. Use the following as a guide for when you’re working out distances in the night sky!
USER INSTRUCTIONS…Make sure to hold up your hand at arm’s length to the sky.
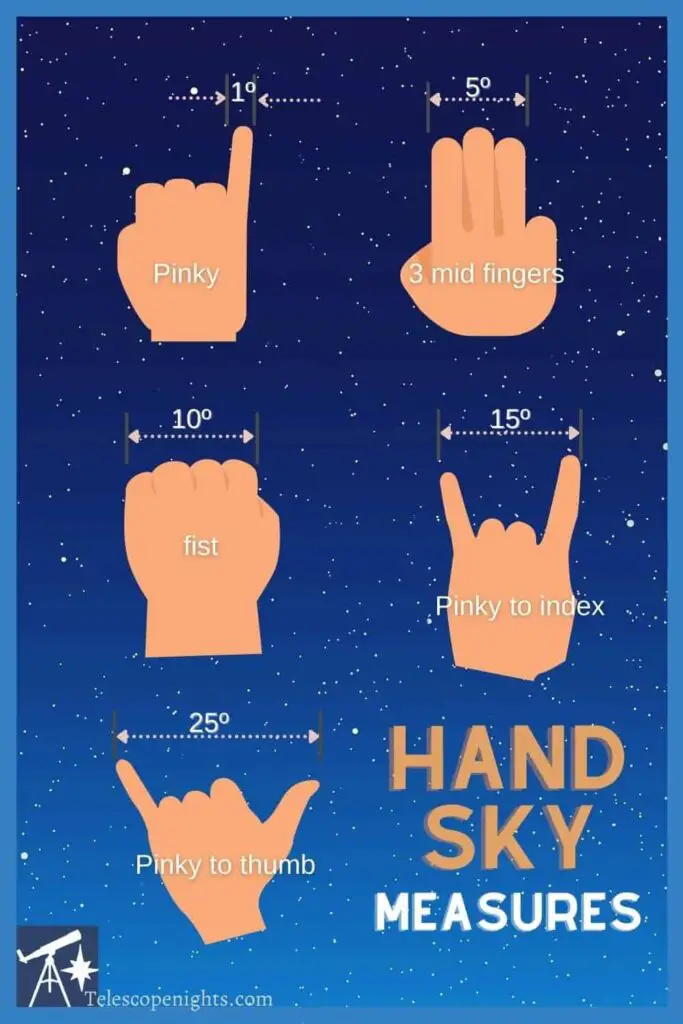
Simple sky Measuring Guide
| 1º | Width of the end of your little finger (pinky) is about one degree |
| 5º | Width of your three middle fingers, tip-to-tip, is about five degrees |
| 10º | The hand width as a clenched fist is ten degrees wide. |
| 15º | The width between your index and little finger, tip-to-tip, when extended from your fist is 15 degrees |
| 25º | That width between your pinky finger and thumb, tip-to-tip when extended from your fist is roughly 25 degrees |
How to get to know your personal sky measures by using your hand to measure angles…
A way to check the span of your hand is to use the Big Dipper or Orion’s seven brightest stars as a gauge.
- Betelgeuse to Rigel in Orion is 19º
- End star of Big Dipper handle to end star of the bowl is 25º
Is your hand span closer to 20º or to 25º?
If you’re in the Southern Hemisphere, look for the Saucepan to located Orion (upside down).
Alternative for estimating degrees above the horizon
Another way to find degrees altitude is to divide the semi-circle into fractions or equal distances matching the angle.
Example:
A planet is known at 45º above the horizon. That’ll be 45º of the 180º altitude arc overhead.
To work out where it sits using the fraction of sky method just divide the semi-circle by the planet’s position and inverse it, i.e. 1/(180º÷45º). The answer is ¼. This means look half way between the horizon and the zenith (90º) — given that the zenith is half-way.
If it was at 22º, it would be about ⅛. Look around the first quarter of the arc between the horizon and the zenith. It’s closer to the horizon.
Some are easier to calculate than others.
How Big Is one Degree in the sky
One degree in the sky is the width of your pinky when held up to the sky at arms length. This is the same as 60 arcminutes, which is the width of two Moons in the sky.
Astronomy measurements are in degrees (º) arcminutes (‘) arc seconds (“), and one minute equals 1/60º and one second equals 1/60’. Put another way, 60 seconds make up a minute, and 60 of those minutes make up a degree. This is a sexagesimal system, not unlike that used to measure time.
It is not unlike the latitudes and longitudes reported as degrees, minutes, and seconds for positioning on Earth. The distance between close celestial bodies is usually down to units of arc minutes / arc seconds.
Also, one degree is equal to 52.5 feet at a 1000 yard distance, when talking about the field of view. This means that what you are seeing at a 1000 yards from where you’re viewing will be 52.5 feet from edge to edge of the circular viewing frame.
Some sky distances in degrees
Measuring a sky object by angles: Let’s take the Sun and the Moon. When looking at the Sun or the Moon, it will be roughly 0.5º in diameter in the sky. In arc-minutes, it’s 32 for the Sun and 30 for the Moon.
Movement across the sky in angles: The Sun moves across the sky 15º each hour (24 hr in a day and 360º in a full circle).
Distance discerning close stars: At night, our naked eyes can distinguish two close celestial bodies if they are at least 6 minutes (one tenth of a degree) apart. Stars or other celestial bodies closer than 6 arc-minutes or a tenth of a degree (e.g. double stars or triple stars) will appear as a single entity, unless viewed through a set of binoculars or a telescope. A 2-inch (60 mm) telescope can discern two equally bright stars if they are at least 2 seconds apart. For a 3-inch (90 mm), this gets better, up to 1.5 seconds.1
- Betelgeuse to Rigel in Orion is 19º
- Orion’s belt is a bit less than 3º.
- End star of Big Dipper handle to end star of the bowl is 25º
- Between two end stars of the bowl: 5º
- The Great Square of Pegasus sides on average: 15º
- The W of Cassiopeia, from one end to the other: 13º
- Sun dogs are 22º from the Sun
Summing it up
Angular distance is the apparent distance from one celestial body to another, measured in degrees or part thereof. A simple convenient way of measure is to use your hand.
The finger and hand distances generally work for everyone because one’s arm length is proportional to their hand size. The exception is the hand-span measure extending the thumb and little finger apart. Some people have more or less flexibility in their thumb than others and so this can vary from person to person.
References
- Dickinson, T. 2019. NightWatch: A Practical Guide to Viewing the Universe. (affiliate link) Firefly Books.
- Time and Date
- Mosley, John. 2003. Starry Night Companion (affiliate link). Space Holding Corp.
